EC220 Problem Set 2
October 21, 2019
This is the second problem set. Let me just take this space to re-iterate that it is nigh impossible to do well in this class ifyou don’t use the textbook.
Book Problems [will not be covered in Seminar]
Tadelis problems 7.1, 7.2, 7.4, 8.1, 8.4, 8.12, 10.2,10.3, 10.6, 10.12
Relevant readings: Tadelis chapters 7, 8, 10
1 More Auctions! [will be covered in Seminar]
Suppose we think of a sequential version of our old Auction game from the last problem set:
. Player 1 places a bid.
. Player 2 observes player 1’s bid, then places a bid.
. The player with the highest bid wins the item at auction.
. In case of a tie, the winner is determined randomly (with equal probability among those tied).
. The winning player pays his bid.
Two players bid for a rare bottle of Laphroaig whiske. This is an auction in which they can bid any amount in R+. Suppose the two players both value the item at $500.
1.1 Find all pure-strategy Nash equilibria of this game.
1.2 Find all pure-strategy Subgame Perfect Nash Equilibria of this game.
Now, we’re going to change the rules a little bit. Suppose that the players can only bid integer amounts of money.
1.3 Find all pure-strategy Nash Equilibria of the simultaneous-integer-bid game.
1.4 Find all pure-strategy Subgame Perfect Nash Equilibria of the sequential-integer-bid game.
2 Extensive Form Extravaganza [will be covered in Seminar, time per- mitting]
Consider the following game, similar to the one from class but with three players.
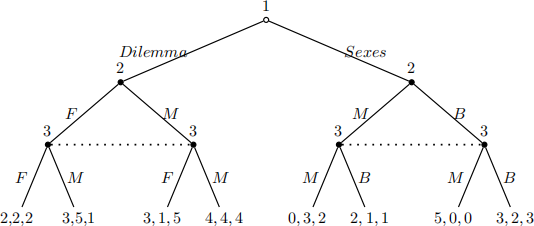
2.1 Write this game in Normal Form and fnd all pure-strategy Nash Equilibria.
2.2 Solve for all SPNEs (pure and mixed) .
3 Repeated Games: Tragedy of the Commons [will not be covered in Seminar]
Suppose N = 3 shepherds all graze their sheep on the same land (of size N). Each day, they can choose to have their sheep either
. Graze sustainably (‘Graze’), or
. Gorge on as much grass as possible (‘Gorge’).
A shepherd’s sheep gain 1 pound of meat if they Graze, or N pounds if they Gorge. Additionally, for each other lock that gorges, aa shepherd’s sheep lose an extra 2 pounds regardless of whether they graze or gorge themselves; there is no loss if other locks graze. Shepherds each attempt to maximize the weight of their own sheep.
3.1 What NEs exist if the game is played only once?
3.2 What SPNEs exist if the game is fnitely repeated?
3.3 Suppose instead the game is infnitely repeated with discounting. Construct Nash Reversion strategies with only Graze being played on-path by all players and fnd the set of discount factors for which these strategies form an SPNE.
3.4 Suppose instead the game is infnitely repeated with N > 3 players. How high does the discount factor have to be for Nash Reversion strategies with only Graze being played on-path by all players to form an SPNE?
3.5 With N = 3, fnd a discount factor and an SPNE for the repeated game with that discount factor where shepherd 1 gets a payof of at least 2 .