CS 188
Introduction to Artificial Intelligence
Summer 2023
Final
Q1. [10 pts] Potpourri: Blast from the Past
(a) Search. Barbie and Ken are in a building of size H × W × L. Each cell of the building mayor may not contain a toy, and
their mission is to collect all of the toys. It is okay for Barbie and Ken to be in the same cell of the building. (i) [2 pts] Propose aminimal state space representation for this problem.
(ii) [2 pts] What is the size of the state space?
(b) [2 pts] CSPs.
Alice is scheduling job interviews. Nine different companies reached out to interview her this coming week, and she is panicked trying to schedule all of them in just five days! For the nine companies, three are big (B1 , B2 , B3), three are medium (M1 , M2 , M3), and three are small (S1 , S2 , S3). Write down her constraints formally below:
|
Index |
Explanation |
Constraint |
|
A |
You should interview with B2 on Friday. |
B2= 5 |
|
B |
You should interview with B3 on Monday. |
B3 = 1 |
|
C |
You should interview with S1 on either Monday or Tuesday. |
S1 ∈ {1, 2} |
|
E |
You should interview with S2 after S1 (cannot be on the same day). |
S2> S1 |
|
G |
You should take at least two days break after M2 before M3 (If M2 occurs on Monday, the earliest M3 can occur is Thursday). |
M3> M2+ 2 |
|
H |
You should interview with M3 after B1 (cannot be on the same day), since they have the same interview style. |
M3> B1 |
(c) [4 pts] Games.
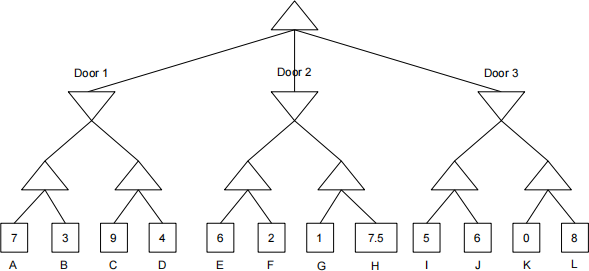
(i) [2 pts] Fill out the values on the game tree. Which door does the top maximizernode choose? . Door 1 o Door 2 o Door 3
(ii) [2 pts] Which terminal nodes are never explored as a consequence of pruning? (Assume that we prune onequality.)
□ A □ B □ C ■ D □ E □ F ■ G ■ H □ I □ J ■ K ■ L
o None of the above
Q2. [13 pts] Bayesian Networks: Across the Spider-Verse
Miles is curious about the probability that he arrives to school on time. The factors involved with him arriving to school on time can be represented by the following Bayes Net (assume that each variable is a binary variable):
• A: Sets alarm
• S: Over sleeps
• D: Dad is late
• T: Arrives at school on time
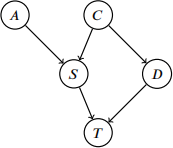
(a) [7 pts] Miles wants to calculate P(C|T) using variable elimination. Assume he eliminates variables in alphabetical order (A,D, S).
(i) [1 pt] What factors does he have available at the start?
(ii) [1 pt] First, he eliminates A, and get the new factor
(iii) [1 pt] Then, he eliminates D, and get the new factor
(iv) [1 pt] Then, he eliminates S, and get the new factor
(v) [1 pt] Finally, join any remaining factors to calculate
(vi) [1 pt] How can he use this to calculate P(C = +c|T = −t)? Your answer should be in terms off4.
The following CPTs correspond to the Bayes Net above:
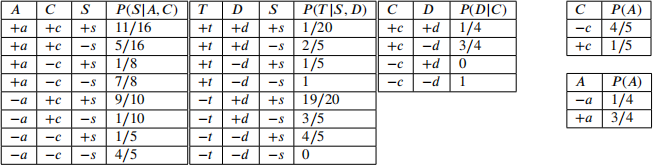
Miles is now interested in calculating P(C = +c|T = −t) via sampling. He generates the following random samples (assume the variables were generated from left to right):
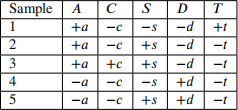
(b) [3 pts] Assuming Miles uses prior sampling:
(i) [1 pt] Bubble in the samples that Miles uses to calculate the final probability.
□ 1 ■ 2 ■ 3 ■ 4 ■ 5
(ii) [2 pts] What is the probability he calculates via prior sampling?
(c) [3 pts] Now assuming Miles uses likelihood weighting:
(i) [1 pt] What weight does Miles assign to each sample?
What final probability does he calculate?
(ii) [2 pts] What is the probability he calculates via likelihood weighting?
Q3. [12 pts] HMMs: Head TA Kirby
Kirby is serving as a TA. He wants to evaluate his teaching performance after each of his weekly discussion sections, and he does so based on how much his students collaborate during his section. He models this situation using an HMM.

Ti is a binary random variable representing whether Kirby taught sufficiently well during Week i. Ci is another binary random variable representing whether students collaborated during Week i. He does not see his students’ collaboration during Week 0.
(a) [8 pts] Using the two steps of the forward algorithm, calculate the distribution of P(T1|C1 = +c). For the sake of organization, you may use the first box for the time elapse update and the second box for the observation update. You may also leave your final answers unsimplified (for example, as fractions).
Time elapse update:
P (T1 = +t|C1 = +c) =
P (T1 = −t|C1 = +c) =
(b) [4 pts] In order to save computational resources, Kirby turns to particle filtering to analyze this HMM.
(i) [2 pts] At timestep t = 3, Kirby has observed the following evidence: C1= +c, C2 = −c, and C3= +c. Following the particle filtering algorithm, assign weights to particles in the following states at t = 3:
Particles in state +t will have weight:
The weight of a particle in some arbitrary state t is P(C3= +c|T3 = t).
(ii) [2 pts] At timestep t = 6, we observe 3 particles in state +t and 5 particles in state −t, and C6 = −c. Fill in the table describing the distribution that weresample our new particles from for t = 7. Show any work in the box on the left.
Q4. [15 pts] Decision Networks: Coin Toss Game
Alice and Bob are participating in a coin toss game. Both playerstoss two fair coins. Bob’s coins are revealed first, after which he must choose to “continue” or “concede”. If he concedes, Bob loses $2 and the game ends. If he continues, Alice’s coins are revealed. If Bob’s coin toss resulted in strictly more heads than Alice’s,he wins $10. However, if he has an equal or lesser number of heads than Alice, Bob loses $10. Assume Bob is rational and his utility is the amount of money he wins.
(a) [2 pts] Sketch the decision network for the game, use the following nodes and node types.
Nodes: B represents the number of heads in Bob’s coins; A represents the number of heads in Alice’s coins; C represents Bob’s choice to continue or concede; U represents Bob’sutility.
Node types: An elliptical node represents a chance node; a rectangular node represents an action node; a diamond-shaped node represents utility.
C U
B A
(b) [3 pts] For each scenario where Bob gets 0, 1, or 2 heads, what should Bob’s decision be: to "continue or "concede"? Justify your answer.
(i) [1 pt] If Bob gets 0 heads:
(ii) [1 pt] If Bob gets 1 heads:
(iii) [1 pt] If Bob gets 2 heads:
(c) [3 pts] What is the expected monetary gain or loss for Bob in a game?
(d) [2 pts] Bob perceives the game as unfair and refuses to participate. To persuade him, Alice proposes an additional rule: Bob can pay Alice c dollars (c > 0) to see one of Alice’s coins before seeing his own coins. Sketch the decision network for the modified coin toss game.
New node: R represents the revealed coin, either head (R = H) or tail (R = T). S represents Bob’s decision of whether to see one of Alice’s coins.
C U S
B A R
(e) [2 pts] Following the previous part, calculate the conditional distribution of A given R and fill in the table:
|
R |
Pr(A = 0|R) |
Pr(A = 1|R) |
Pr(A = 2|R) |
|
H |
|
|
|
|
T |
|
|
|
(f) [3 pts] (Extra Credit!!!!!, do this last) Following the previous two parts, Alice secretly insists that this new rule should not impact her expected gain. What should the value of cbe to meet this condition? Justify your answer.