Volatility Forecasting Homework
October 26, 2023
1. You will estimate the parameters of a few GARCH-type models using SPY data (the S&P 500 ETF) from February 1, 1993 to Oct 20, 2023. I would like you to build this from scratch, rather than use a package.
(a) Estimate the parameters of a GARCH(1,1) model. Compute the maximum value of the likelihood function.
(b) Estimate a GARCH(1,1) model with conditional returns having a Generalized Error Distribution. Compute the maximum value of the likelihood function. Using the Schwartz Bayesian Criteria, does the higher likelihood compensate enough for the extra parameter?
(c) Estimate a TGARCH(1,1) model with conditional returns having a normal dis- tribution. Compute the maximum value of the likelihood function. Using the Schwartz Bayesian Criteria again, does the higher likelihood compensate enough for the extra parameter compared to the GARCH(1,1) in part (a)?
One way to download historical prices for SPY in Python is to pip install the yfinance library and download the data using
import yfinance as yf
df = yf. download("SPY", start=’1993-02-01’, end=’2023-10-21’)}
Use the ”Adj Close” column, which adjusts for dividends.
2. One of the big trends in options this year is the dramatic rise of trading in zero-days- to-expiry (0DTE) options . These are options that expire within 24 hours. Options that expire every day of the week are now available for popular securities like SPY and QQQ. According to the CBOE, 44% of the S&P500 option volume is for options with less than 24 hours to expiration, for a notional amount of over $500bn traded per day.
The figure below lists prices and implied volatilities for puts and calls on SPY options as of the close on Friday, October 20, 2023. The middle column are the strikes, and the data on the left side are for the call options, and the data on the right side are for the put options. The first five rows are for options that expire the following Monday, one trading day later.
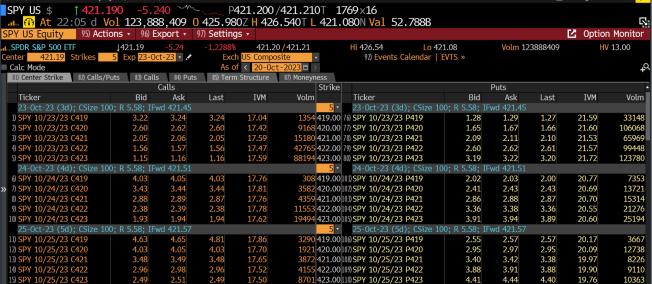
Figure 1: Daily Option Prices at the Close on Oct 20, 2023
Use the GARCH model in part (a) and the TGARCH model in part (c) above to price the 421 straddle (a straddle is a combination of a put and call at the same strike and expiration). You should price the straddle using Monte Carlo simulations over a one-day horizon. Explain how you get the volatility forecast from Friday to Monday. Notice that the market price of this straddle is 2.05+2.10 = 4.15. Do the models want to buy or sell the straddle? The TGARCH model should place a higher value on these options. Give a one sentence explanation why.
As a pure bonus, you can try a GARCH model with a day-of-week dummy variable.] to potentially account for the possibility that volatility varies by day of the week. This is very tricky and you might not be able to get it to work. If you do try this and feel like you got it to work, feel free to email me your code.
A few additional comments:
. The SPY options stop trading at 4:15pm, whereas SPY stops trading at 4:00pm. On Friday, the closing price of SPY was 421.19 at 4:00 but went down to 421.08 by 4:15 when the options closed. However, since we are pricing a straddle that is close to delta-neutral, adjusting the starting price of SPY will not affect the value of the straddle: the put will be worth a little more and the call will be worth a little less.
. On that Friday, there were rumors that the Middle East fighting would escalate over the weekend. The market may have been pricing in some additional risk. Obviously, GARCH-type models can’t take these factors into account, since they just use historical returns.
3. In class, I mentioned that Ordinary Least Squares (OLS) is a special case of GMM. In this exercise, you will verify that. Consider the linear regression model
yi = α + βxi + ϵi
where ϵi has a mean of zero and a variance of σ2. The sum of squared residual errors is
SSE = ![]() [yi − (α + βxi )]2
[yi − (α + βxi )]2
and in OLS, we minimize the SSE by taking the partial derivatives of SSE with respect to α and β . Use those two equations to form moment conditions (in this case, M = P = 2). Simulate some data for a given α and β, and use GMM to estimate those two parameters. You can also verify your results by doing a linear regression:
import statsmodels. api as sm
X = sm.add_constant(x)
model = sm. OLS(y,X)
results = model. fit()
results. params
4. In class, we talked about the paper “An Empirical Comparison of Alternative Models of the Short-Term Interest Rate” by Chan, Karolyi, Longstaff, and Sanders (CKLS), where they estimate parameters for eight popular models of short-term interest rates using GMM. In this exercise, you will replicate their study on one of those models.
(a) Estimate the four parameters of the unrestricted model.
(b) Estimate the two parameters in the Geometric Brownian Motion (GBM) model.
Just like with the other excercises, I would like you to estimate the parameters from scratch, rather than using a package. I have attached one-month interest rate data from WRDS (the start date of 1964-06-30 and the end date of 1989-12-29 was chosen to match CKLS). I am also attaching the original CKLS paper. I was able to match the parameters of Table III of their paper relatively closely, but not exactly. In order to match the parameters, the data needs to be scaled correctly. First of all, you should divide the interest rates by 100, since 5% is represented as 5.0 and not 0.05. You should also include ∆t = 1/12 in the moment conditions. In other words, the first moment condition, for example, should be:
E[rt+1 − rt − (α + βrt )∆t] = 0
and the third moment condition should be:
E[ϵt(2)+1 − σ 2rt(2)γ ∆t] = 0
Also, to make things easier, you can choose to do two-step GMM rather than iterated GMM, and you can compute the weighting matrix assuming the data are uncorrelated so you don’t have to compute the Newey-West adjustment if you would like. You may have to vary the initial parameter guesses because sometimes the optimizer gets stuck in a local maximum that is not the global maximum.