STAT0023: general feedback for in-course assessment 2
2022-23 session
This assessment was intended to be challenging. This is partly to compensate for the straightforward Moodle quiz assessments, but also partly because the material in STAT0023, in combination with that from your other ‘core’ statistics modules, gives you the skills needed to tackle complex real-world problems — and the ability to do this is a key outcome of any degree programme involving statistics or data science.
This is the first time that most of you have been asked to produce an extended piece of statistical work on this scale. It is clear that many of you put a lot of work into it, and that you used the support that was offered (hints, drop-in hours, discussion forum etc.). Hence most of the reports were reasonably well written and analyses were broadly sensible.
On the minus side, a substantial minority of submissions had careless and basic errors and misunderstandings; and there weren’t many really excellent submissions. For an assignment like this, ‘excellence’ requires: (i) creativity and awareness, rather than just following examples that you’ve been given; (ii) thinking about the problem carefully; and (iii) using the whole range of statistical and computational skills that you have been taught. This is difficult, particularly if you haven’t done it before. We hope you learned something from the experience, and also that this feedback will help to highlight some common mistakes so that you can avoid them in the future.
Most people managed to follow the instructions with respect to naming the files in their submissions. A substantial minority (again) didn’t: it’s hard to understand this. You might think that it doesn’t matter, but we need to process each submission (for example, to calculate the scores for your predictions) and, with 510 files submitted in total, we need a systematic way of distinguishing between them.
Your individual feedback and provisional grades can be found on the ICA2 Moodle page: for each of you, the feedback is in a file called Feedback.txt which should be visible alongside your submission. If you can’t see it, it has gone off the right-hand edge of the Moodletab: in this case, you may be able to reveal it by hiding the blocks — there should be an option to do this at the top-right of your Moodle page. Otherwise, try making the text smaller by pressing and - (that’s “Control-minus”). As with ICA1,the feedback consists partly of a set of automated checks, and partly of some individual comments that are intended to help you see what you did well and what you did less well.
1 Coding
Nobody used SAS for this assessment: everyone used R. We were pleased to see that almost everyone is comfortable using R to read and manipulate data, carry out basic — and in some cases, quite advanced — statistical analyses, produce graphs and so on. If you got a “B” grade or above then you have the computing skills that will enable you to survive if you get a job involving analytics in some way. Conversely, if you got a “C” or below then you need to work on your computing skills if you’re aiming for this kind of career.
A disappointing number of submitted scripts (25 out of 96) didn’t run as submitted, for various reasons of which the most common were trying to change the working directory within the script and trying to access the data from a specific location on your machine that doesn’t exist on ours (the assignment instructions were clear about this). After correcting the scripts where possible, 18 of 96 failed to produce a file containing the submitted predictions. In most cases, this was because they didn’t produce an output file at all. Given that the predictions were worth up to 20 marks out of 75, it was slightly surprising that so many groups didn’t ensure that they were produced as requested. Moreover, the predictions were formatted incorrectly in 10 of 96 submissions.
The assignment instructions also state that “you will only receive credit for the graphs in your report if your submitted script / program generates and automatically saves all of these graphs when it is run” (emphasis added). 44 out of 96 submissions failed to achieve this. Common reasons for it included failing to enclose ggplot() commands in a plot() or print() statement (or using ggsave()), and failing to usedev.copy() or similar to export the graphics to a file. Both of these were covered during the Week 1 workshop. It is possible that some of you don’t understand what is meant by “running” a program, and that you pasted your commands line-by-line into the console instead of source()ing your script. Again, this was covered very early in the course. The task may have been challenging, but you must never forget the basics!
There were a few groups who made two or more of the mistakes above, and who lost many marks as a result. You may feel that this is harsh, but ultimately it shows that you need to improve your basic IT skills: effective use of computers, and understanding of why these things are important, is essential in any modern quantitative environment.
Some more specific comments and hints on coding are as follows:
• As noted above, many groups submitted code that needed correcting before we could run it. In some cases, the code relied on objects that didn’t exist, or contained typographical errors so that it could never run on any machine. If you have to write code in the future (e.g. for your employer), we recommend that you test it in a ‘clean’ environment by first removing all objects from your workspace (rm(list=ls())) and then source()ing your script: if your code runs without error in this case, and it doesn’t contain any references to files or folders in specific locations on your machine, then it should work for other people too. However, you should not include rm(list=ls()) INSIDE your script! That will wipe out anything the user may have had in their workspace, and they will not thankyou for it.
• For an analysis such as this one, you often need to repeat tasks multiple times under slightly different settings (e.g. produce plots of the response variable against a large number of different covariates, perhaps with the points coloured according to the value of some factor such as Region). In this case, if the task itself requires a few lines of code, it’s worth writing a function to do it: this means that you can execute the task subsequently with a single command, which makes your code more compact and easier to read. Few of the submitted scripts made effective use of functions or other programming structures: many looked like sequences of commands that could be typed at a prompt, instead of making full use of the programmer’stoolkit.
• When you write code that is designed to be source()d, you should use cat() and print() to ensure that any output appears when the code is run. Many submitted scripts produced nothing on screen when they were run! Again, this was covered during Week 1 of the course. It’s less helpful to use View(), because it forces the user togo into another tab where the object is shown.
• Several groups created and saved large numbers of individual plots, and then had to import them into Word (or whatever) when writing their reports. It can often be time-consuming to import large numbers of graphics files into Word and similar packages; and it can be extremely frustrating to try and get them to align correctly. If you’re using R to generate your graphics therefore, it’s far better to use par(mfrow=c(r,c), ...) to generate a single graphics file in which the plots are laid out in an array with r rows and c columns. Sometimes it’s helpful to change the default plot margins when doing this. There were several examples in the early weeks of the course.
• Several groups used packages that were not permitted, and were penalised appropriately.
• Many of the scripts showed that you have spent a significant amount of time reading up on the internet on techniques that we haven’t taught you. This is great, in general. However, some of you have perhaps spent less time studying the material we DID teach you! For example, many groups fitted a Binomial/Quasibinomial GLM but forgot to use the weights argument (see Week 6 materials)!
• Quite a few people lost marks for using row and column numbers, rather than identifying the rows/columns by their name or characteristics. This is very dangerous, because you might subsequently decide to insert an extra column somewhere: if that happens, you must then go through your entire script, check that all the numbers are still correct and change them if necessary. It is also prone to errors (you might mis-count), and it makes the code hard to read.
• A few groups used PCA or clustering on their data. However, some of these groups fitted PCA and clustering separately on the “known” and “unknown” part of the data: this doesn’t make sense, because if you use a regression model to predict the unseen data, you need to use the exact same principal components and clusters that you used to create the regression model.
• A few groups used attach() in their code, to make the code easier to read. However, attach() can create problems, because the variable names might clash with existing variable names the user has in their workspace. Instead, consider using short but clear object names to make your code less cluttered.
2 Reports
Writing an extended report is hard work, even for those of us who have been doing it for many years: you have to decide what to exclude, and then organise everything into a coherent narrative that is accessible to the reader. Hopefully this exercise has given you some experience — and some ideas for improvement — that will be useful for you in the future. Almost all of the reports were written well, with a clear structure and, in most cases, a recognisable argument leading from exploratory analysis through to modelling and final conclusions. The best reports incorporated external information as well (such as the insights from Martin Rosenbaum’s article) to guide the analysis — but not to dictate it!
The reports suggest that many of you have a reasonable operational understanding of linear and generalised linear models — and even GAMs, in some instances. Many submissions used a quasibinomial model to account for overdispersion (well done for spotting this), and used a wide variety of criteria to help choose a model (e.g. p-values, nested model comparisons and residual plots). This shows a good level of basic technical competence with the statistical methodology, at a level that will be at least as good as your peers / competitors when you’re entering the job market.
We were also pleased to see that most of the exploratory analyses focused on the relationship between the response variable and covariates — this was not always the case in previous years. Thus, most submissions provided plots of the response variable against the covariates and made sensible comments about these plots. As a reminder: the reason for producing such plots is to provide provisional answers to questions such as “Could there be a relationship between this covariate and the response?” and “If so, could the relationship be linear on the scale used for subsequent analysis?” .
In a task like this however, there is always room for improvement. The difficulty of doing good applied statistics is often underestimated; often the most basic things are overlooked. The comments below may be useful if you have to carry out a similar task in the future.
2.1 Choice of material
When you have limited space to present an argument, you can’t afford to waste it on things that aren’t absolutely relevant. So you need to focus on the most important messages. As an example: many groups wasted space in their reports repeating material from the question. Others wasted graph / table space on non-essential plots. You don’t need to provide all of your plots: just those that illustrate key messages, or that provide reassurance that you know what you’re talking about. It’sfine, for example, to say something like “Figure XX shows the relationships between the response variable and a selection of covariates; similar plots (not shown) have been examined for all of the other covariates” .
2.2 Use of contextual information
Few submissions obtained all 5 marks that were available for demonstrating awareness of the context in their analysis. Many didn’t seem to consider it at all. Of those who did, it wasn’t always clear that contextual information was being used to inform modelling decisions. For example, it is helpful to check that the results of a model comparison make sense, given what is known about factors influencing people’s voting tendencies.
Conversely, there were cases where people used their “understanding” of the context to choose covariates without checking whether their decisions were supported by the data — and, often, based on superficial reasoning. A common example involved discarding the variables relating to age categories under 18, on the grounds that children can’t vote. But wards with large numbers of children are likely to have many young families: this is demographic information that could be relevant.
It was nice to see many people doing background reading, for a better understanding of factors that are thought to have influenced the referendum result. Be aware, though, that if you do this then it’s not enough just to list your references at the end of the report: you need to cite them at the point where you use the information, or the reader will have no idea what you have used them for! Also, you should provide enough information that the reader can quickly find the references (look at examples from published papers) and, for longer references such as books and reports, the particular part of the reference that you have used. Many of you provided URLs, which was very helpful.
2.3 Graphs and tables
There were few really good graphs. By “really good”, we mean that they are carefully chosen to highlight the most important messages, and that they are carefully presented so that those messages stand out very clearly and immediately. Based on what we have seen, some tips for the future are:
• Think about the reader. Reports are written to be read. When you write therefore, you must put yourself in the position of a reader. A disturbing number of submissions handled the two-page limit on graphs and tables by including far too many of them, and reducing the size so that they were barely legible. What’s the point of including graphs or tables that nobody else can read?!
There were other cases where, although the graphs themselves were of a reasonable size, the axis labels, titles and / or legend entries were too small to be readable without magnification. Again: think. These are simple things, but they are easily overlooked.
• Design your graphics to use the space effectively. If you take the question seriously, you need to visualise a huge number of potential relationships to inform your analysis — but you only have two pages to do this. One solution is to cram it all in by shrinking everything down to a tiny size, but — as noted above — this is not very helpful to the reader. As an alternative: unleash your creativity! Good statistical graphics are designed, to convey the maximum amount of information in the minimum amount of space.
For example: many of you produced scatterplots of the ‘Leave’ vote proportion against each of the numeric covariates, and then produced boxplots to show the distribution of vote proportions within each of the administrative regions or area types. You could save yourself some space here, by using different colours or symbols to represent regions / area types in your scatterplots. If you do this, there’s no need for the boxplots — any differences between regions or area types will be obvious from the scatterplots.
Sometimes it isn’t enough just to use colour or plotting symbols to distinguish between groups on a scatterplot. It’s OK for a small number of observations or if the groups are well separated, as in the iris example considered earlier in the course; but it can be hard to spot patterns in a messy data cloud. In such cases, it’s helpful to add group-specific nonparametric regression curves to the plot as well. Figure 2.1 gives an example: this isn’t intended to be definitive, but hopefully it illustrates the amount of information that can be condensed into a relatively small amount of space.
• Provide informative captions. All figures and tables should be accompanied by a
caption that describes exactly what is being shown, clearly and precisely. The aim is to ensure that the figure or table can be interpreted immediately by a reader, without having to search through the report to figure out what is being presented. Consider Figure 2.1 for example: how well would you understand this without the caption?
2.4 Modelling
A very wide range of models was used — see the “Prediction” section below. Some groups considered just two or three models in arriving at their final choice, while others considered many more — which is probably necessary to do justice to the problem.
Common issues that arose in the modelling were as follows:
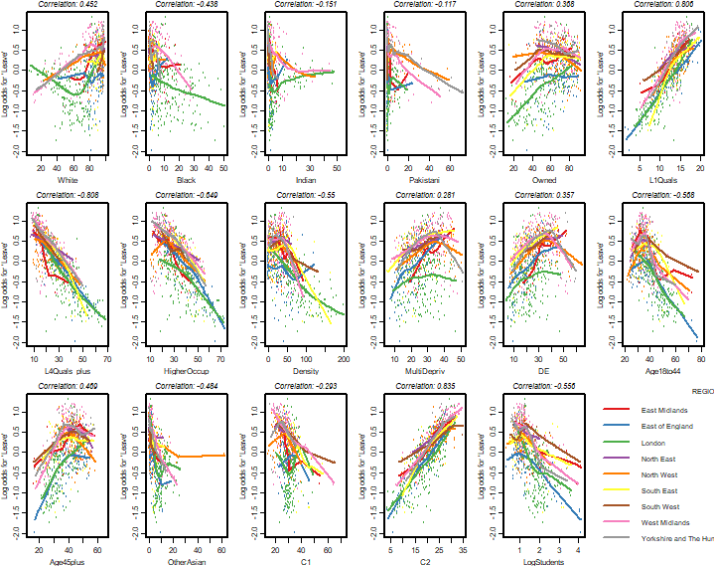
Figure2.1: Relationships betweenthe logoddsforvoting ‘Leave’and an initial set of covariates identifiedvia preliminary screening. Covariate namesaregiven beneath each plot,andthe overall correlation isgiven above. The region-specific nonparametric regression curveson each plot are obtained usingthe lowess()command in Rwith default settings.
• Choice of distribution: a surprising number of submissions used GLMs or GAMs based on the Poisson or negative binomial distributions, on the grounds that the number of ‘Leave’ votes is a count. This argument doesn’t really make sense: yes, the response is a count, but it can’t be larger than the total number of votes. Perhaps many of you have forgotten that the Poisson is an approximation to the binomial when n is large and p is small? This approximation is unlikely to apply here, because p is not small.
Some of you tried Poisson or negative binomial models after trying binomial or quasibinomial models and obtaining results that didn’t make sense. Well done for noticing that the results didn’t make sense. Not well done, though, for failing to spot that this was caused by your own errors! The problem was almost always caused by forgetting the weights argument to the glm() command (see earlier “Coding” feedback).
• Most of you checked your modelling assumptions at some stage: this is good. But many of you didn’t do this until you had already fitted several models and made decisions about which covariates to include. This is dangerous: you need to check assumptions early on (e.g. after fitting your initial model), to ensure that your modelling decisions are roughly correct. The reason for this is that your decisions are based on things like AIC values, deviances and ,-values; and all of these things rely on the assumptions.
A common example of this problem related to overdispersion — at least, for those who started with binomial or Poisson GLMs. The data are massively overdispersed: unless you account for this from the outset, much of your intermediate modelling will be incorrect.
• It’s always worth revisiting the conclusions from your exploratory data analysis after a first round of model-building. You may find that more subtle relationships appear after you have accounted for the most important ones: you can check for these by plotting the residuals from a “first round” model against all of the covariates.
A related point is that several people seemed to be looking for models that confirmed the results from their exploratory data analysis. This shows some misunderstanding. One aim of an EDA is to find a sensible starting point for your modelling: this is essential, but you can’t uncoverall of the structure in a dataset using EDA (if you could, why build models?!). Sensible models offer much more detailed insight than is possible in an exploratory analysis, because they account simultaneously for all of the covariate effects.
• Some people are confused about interactions but don’t realise it. Do you think that
potential correlation between covariates implies that you should include the corresponding interaction term in a model? If so, you have misunderstood the concept. To refresh your memories, look at the Week 2 lecture slides, together with the ‘iris’ example from the Week 2 self-study materials and (perhaps) your STAT0006 materials.
• Very few people thought carefully about the interpretation of coefficients associated
with factor covariates such as RegionName and AreaType; and nobody used sum-to-zero constraints for these factors, despite the lack of an obvious reference level for them. This was a bit disappointing.
• Among those who used GLMs, there was some misunderstanding about how to interpret the coefficients. A few groups obtained intercepts outside the range (0, 1), and claimed that this was a shortcoming of their model because the response variable is a proportion — but the intercept in a GLM isn’t on the scale of the response variable, it’s on the scale of the linear predictor. If you use a logit link for example, the intercept represents the log odds when the covariates are all zero: the log odds can take any real value.
A similar type of mistake was made when interpreting the coefficients in a GLM. For example, several people made statements along the lines of “all other things being equal, a 1-unit increase in [some covariate] is associated with an increase of [whatever] in the probability of voting ‘Leave’”. This is incorrect: the association should be with an increase of [whatever] in the linear predictor. For example, if you used a logit link then the association is with an increase in the log odds.
• When discussing model limitations, several groups cited collinearity as a potential
problem. This is not necessarily true. The standard errors of the model coefficients would be smaller in the absence of collinearity; but if they’re small enough already then it’s nothing to worry about.
• Many people used hierarchical clustering and principal components analysis; and the
majority did it in almost exactly the same way as was demonstrated during the Week 10 lecture. This was really silly! See general comment above, about being creative rather than just following examples that you’ve been given (and strong hints were given, during and after the lecture, that you probably shouldn’t do exactly what was demonstrated).
Why is it silly to follow the examples from the Week 10 lecture? Well, the ‘ethnicity’ PCA example isn’t so silly, but the clustering example is. Remember: the purpose of the analysis is to learn about variation in the ‘Leave’ vote proportion — so what’s the point of doing a clustering analysis based on the covariates? All this does is to create new groups that duplicate information that is already present elsewhere! In our specimen solution, we started by fitting models including RegionName as a factor; and then we did clustering based on the resulting region-specific coefficients. The effect is to combine regions with similar coefficients, so that we can simplify the model without losing much information.
• A few groups noticed that there were some outlying wards on the basis of their residual analysis, and removed them before refitting the model. This is a really bad idea! It gives you false confidence because you’re making the data fit the model, and it’s particularly serious when using your model for prediction. There is no reason to think that the vote counts in the outlying wards were incorrect, so there is a good chance that similar outliers will exist in the unseen data which you’retrying to predict. If you fit your model after removing the outlying wards, then your prediction standard errors will be too small — and (hopefully!) you will be punished for this via your prediction score.
3 Predictions
In your individual feedback, you will all find your prediction score and your rank in the class. We also calculated your root mean squared prediction error, defined as
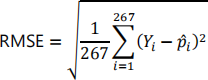
using the same notation as in the question sheet. This is a more common measure of prediction performance than the score S that we used to assign your marks: the reason for using S is that it accounts for your prediction standard errors as well, and rewards those of you who gave an honest assessment of your prediction accuracy.
If you’re interested in knowing the real values for your predictions, we have uploaded a file VoteProportions.rda to the Moodle page. If you load this into R using load("VoteProportions.rda"), you will find a data frame in your workspace called VoringProportions: this is the complete set of referendum results, with a column called PropLeave containing the actual proportions of ‘Leave’ votes for all 1070 electoral wards.
There was substantial variation in prediction performance. Nobody achieved better S scores than us, although one submission achieved a better RMSE (0.04378 vs 0.04385). There were also some much less accurate predictions. Figure 3.1 shows your scores and RMSEs for all scripts, also showing the performance for our specimen answer. There is a massive range of scores, so the successive plots in the figure “zoom in” to enable you to see more relevant detail.
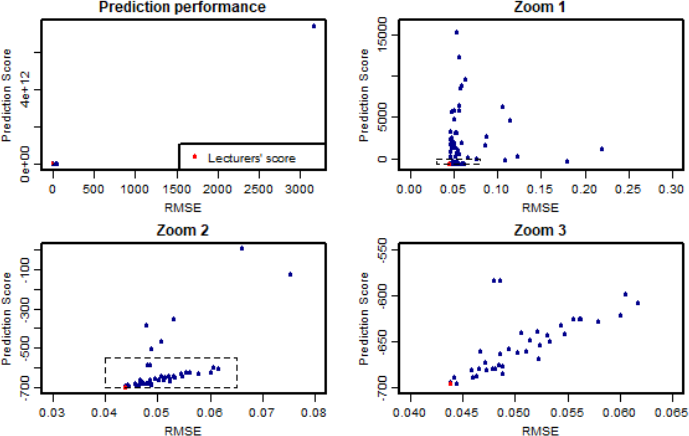
Figure3.1: Performance ofthe predictionsfromthe submittedscripts. The horizontal axis in each plot representsthe root mean squared error ofthe predictions, andtheverticalaxis is the scoreSthatwas usedto assign marksforyour predictions. Thetop left panel showsthe performancefor all submitted scripts:the remaining plotszoom in on successively smaller regions correspondingto better(i.e. lower)scores. Inthe second andthird plots, thezoom region is indicated by a dashedrectangle.
It’s also worth pointing out that the overall standard deviation of ‘Leave’ vote proportions is around 0.15: so anyone with a RMSE greater than this is doing worse than somebody who didn’t build a model at all. Of the 90 groups who submitted readable pediction files, 7 achieved this. You should be quite embarrassed if you’re a member of one of these groups — and you should be very careful in the future when building models, particularly if you’re going to use them to do things like predict investment returns!
The score and RMSE for our specimen solution were -696.1 and 0.044 respectively. We used a quasibinomial GLM with a logit link, and our model has 56 coefficients including the intercept. It contains a mix of covariates, many interacting with a new “Region Group” factor with five levels. We experimented with the use of principal components, but found that they didn’t really help to simplify the model in this particular case. Interestingly, our model didn’t support the idea of an association between older voters and ‘Leave’ votes: according to the model, this apparent association is due to other demographic characteristics of the wards containing large numbers of older voters. We can’t be 100% sure about this conclusion of course; but a model is always more credible if it produces reliable predictions (and it was interesting that several other submissions came to the same conclusion). If you would like to find out more about our specimen model, come to office hours.
We can’t go through every single model in detail here, but you may be interested in the prediction performance of the different types of models that were used. Figure 3.2 shows this. The top panel shows all of the 。scores below 15,000: you can see from this that several different model types were able to produce both good (i.e. low) and bad (i.e. high) scores (there is one model type with no points on the plot: for this type, there were no submissions with scores below 15,000). The ability of several different model types to perform well suggests that — within limits — the choice of covariates is more important than the precise distributional assumptions of the model.
Having said that: the second panel in Figure 3.2 zooms in on the left-hand end of the distribution. Here, you can see that the best scores were obtained from quasibinomial GLMs and linear models. Note that the binomial GLMs performed poorly in terms of the 。score, although some of them did reasonably in terms of RMSE (see bottom panel of Figure 3.2).
This means that these models have the potential to produce reasonable predictions, but do not provide accurate uncertainty assessments because they do not account for the overdispersion in the ‘Leave’ vote proportions.

Figure3.2: Prediction performance by modeltype. Each cross represents one group’s submission:the red dot isfromthe specimen solution. Thetoptwo plots showthe distributions ofthe scoreSthatwasthe basisforthe marking scheme:thetop plot shows submissionswith scores below15,000, andthe second plot shows submissionswith scores belowzero. The bottom plot showsthe root mean squared error(RMSE)by modeltype,for submissionswith aRMSE below0.065.