You should refer to sections 5 and 7 of the Undergraduate Students’ Handbook for details of the University policy regarding late submission and plagiarism; the work handed in must be entirely your own.
It is expected that marking of the assignments will be completed by the beginning of the summer term.
1 Introduction
This assignment involves the development and use of a class to store arithmetic expressions in binary trees. For example, the expression (A+3)/4 would be represented by the tree
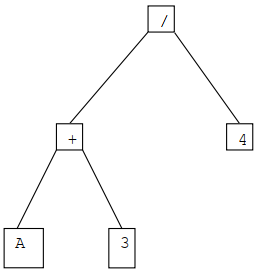
Note that parentheses are not shown in the tree – the expression A+(3/4) would be represented by a different tree with + at the root.
In this assignment the expressions can contain identifiers (comprised of one of more upper-case letters), numbers (non-negative integers) and the six operators +, -, *, /, % and ^.. The / operator denotes integer division ignoring the remainder s 7/3 has the value 2 and the ^ operator denotes power so 2^3 denotes 2 cubed and has the value 8. [n^0 is defined to be 1 for all values of n and n^m does not have an integer value when m is negative.]
2 The ExpTree Class
There are three kinds of expression tree: number leaves containing a non-negative integer
identifier leaves containing a string comprising upper-case letters
operator nodes containing an operator and references to left and right children
Provide in a file called ExpTree.java a class called ExpTree with appropriate constructors. You may use either of the approaches described in part 6 of the lecture slides.
To allow the contents of a tree to be inspected we need a facility to generate post-order output. Post-order has been chosen since this gives a unique output for each tree without the use of parentheses, e.g. the post-order outputs for the two expressions seen on the previous page would be A 3 + 4 / and A 3 4 / +, whereas if an in-order traversal without parentheses was used both would have output A+3/4. Note that spacing is necessary in post-order output since numbers or identifiers can appear in adjacent positions.
You should add a method to the ExpTree class to allow the production of post-order output. This could produce output directly or alternatively generate and return a string that can then be output using System.out.println. If you choose to write a method that returns a string you must not call it toString (a different toString method will be required later in the assignment).
3 The main Method
A Parser class is provided on Moodle with a method called parseLine to generate and return a tree from an arithmetic expression typed on a single line on the keyboard. To use this class you could use code such asParser p = new Parser();
and
ExpTree myTree = p.parseLine();
Write in a file called Ass2.java a class called Ass2 with a main method that outputs your registration number, gives an introductory message to the user, creates a Parser object and then (in a do loop) uses the parseLine method from the Parser class to input an expression and generate a tree, and uses the method written in part 2 to output the contents of the tree in postorder.
The user should then be given the option of quitting the program or entering another expression. User input must be obtained using the getLine method from the Parser class; since the parser has created a buffered reader object, it would be inefficient to create another one to obtain the input.
A typical interactive session might look like
Reg number 1954321
Welcome to Fred’s expression evaluation program. Please type
an expression
(A%3)*(2-BC^(13));
Post-order: A 3 % 2 BC 13 ^ - *
Another expression (y/n)?
n
The user input has been shown in bold – note that the parseLine method expects the user to terminate the expression with a semicolon and will throw an exception of type ParseException if the input is invalid – you should catch this exception inside the body of the do loop before offering the try again/quit option (so a parse exception should not cause the program to terminate).
It will be necessary to modify the supplied Parser class so that eight methods near the end of the class use your constructors to create new trees. These methods are clearly identified within the file Parser.java; you should not make changes to any other part of this file.
4 Evaluating Expressions
The next requirement is a facility to evaluate expressions – for example the value of (3*4)+5 is 17 whereas the value of 3*(4+5) is 27. The value of (A+3)*4 depends on the value of the identifier A.
Add to the ExpTree class an evaluation method that returns an integer. At this stage you should assume that the value of the identifier is determined by its first letter; all identifiers beginning with the letter A have the value 25, those beginning with have the value 24 and so on (with those beginning with Z having the value 0). Hence the evaluation method should return the appropriate value between 0 and 25 when applied to an identifier leaf. When applied to a number leaf the
method should return the number stored in the leaf. When applied to an operator node the method will have to make recursive calls to evaluate the two children and then perform appropriate arithmetic (dependent upon the operator). If the value of the right child of a ^ node is negative an exception should be thrown.
Integer arithmetic should be used in all cases, so for example 7/2 should have the value 3, not 3.5.
Add to the body of your loop in the main method in the Ass2 class (after the post-order output) a try block that contains a statement that calls the evaluation method and outputs the result that it returns (preceded by an appropriate message string). This should be accompanied by a catch block that displays an appropriate message if any exception has been thrown. (Note that an arithmetic exception may be thrown if, for example, an attempt is made to divide by zero, in addition to any exception thrown for a negative operand of ^.)
5 In-Order Traversal
The next requirement is a toString method that uses an in-order traversal. As seen from the two expressions in section 1, parentheses are necessary to avoid ambiguous output. To gain maximum marks parentheses should be displayed only where necessary – for example if the input expression was ((A-3)-(BC-5)) the string generated by the toString method should be A- 3-(BC-5), whereas if the input expression was ((A-3)*(BC-5)) the string that is generated by the method should be (A-3)*(BC-5). No spaces are necessary in the string. The operators +, -, *, / and % should be regarded as having the same precedence as in Java; the ^ operator has higher precedence than any other operator and associates to the right so, for example, A-3^B means A-(3^B) and A^B^2 means A^(B^2).Output that contains unnecessary parentheses will earn more marks than output with missing parentheses so a method that generates the string (A 3)-(BC-5) for the first input expression above would gain more marks than one that generates A-3-BC-5.The main method in the Ass2 class should be modified so that the string generated by the toString method is output (preceded by an appropriate message) after the post-order traversal but before the result of the evaluation.
6 Handling Identifiers
The final requirement is a modification of the program so that the user can supply values for identifiers as part of the input expression. An input expression can now be of the form let A = 3^2 and BX = 0-5 in (A+3)*(2+(A+BX)/3);The expressions on the right of the = signs are not allowed to contain identifiers.
The parseLine method will successfully parse input of this form, generating a ‘let’ tree with the identifier/value pairs in the left child and the main expression in the right child. The left child may be either an ‘equals’ node or an ‘and’ node; the children of the latter may be ‘equals’ nodes and/or more ‘and’ nodes.
You will need to add extra node kinds to the ExpTree class for ‘let’, ‘and’ and ‘equals’ nodes. The ‘let’ and ‘and’ nodes will hold no data. For the ‘equals’ nodes you may choose to either have two children, one for the identifier and one for the expression giving the value of the identifier, or just one child for the expression, with the identifier being stored in the node itself.
Three more methods in the Parser class will need to be modified so that they use your constructors to create new trees.
You should ensure that the post-order output and toString methods still work when the tree contains the new kinds of node; for the post-order method it is acceptable to simply ignore the left child of a ‘let’ node, but the toString method should display the entire input.
In the main method, if the root of the tree is a ‘let’ node the left child should be traversed before evaluation of the right child, with values for identifiers being evaluated and stored in an appropriate data structure (e.g. a map or a list of pairs; you may use classes from the Collections Framework if you wish). In the evaluation method for identifier nodes you should now look up the values of identifiers in this data structure. If an identifier that has not been given a value is used a warning message should be output and the value of the identifier should be assumed to be 0. However, the evaluator should still work in the same way as before if the user has input an expression that does
not begin with the let keyword. (One way of ensuring that this happens, assuming that you are using a map, is to initialise the map to null if the root of the tree is not a ‘let’ node, then simply check in the evaluator if it is null.)