Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MAST10007 Linear Algebra, Semester 1 2024
Written Assignment 4
Symmetries of the Regular Tetrahedron
Let
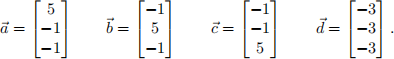
Task 1: Convince yourself that the convex hull of these four vectors,
T = {αa + βb+ γc + δd| 0 ≤ α,β,γ,δ ≤ 1,α + β + γ + δ = 1},
forms a regular tetrahedron, centered at the origin.
Write each of the three standard basis vectors of R3 as a linear combination of a, b, c and d.
This question is not marked and you do not need to show your work for it, but you will want
to use your answer below.
We will write A for the face containing the vertices ⃗c, b and d.
We will write B for the face containing the vertices a, c and d.
We will write C for the face containing the vertices a, d and b.
We will write D for the face containing the vertices a, b and c.
(a) Is the set ⃗a, b, c, d}
Linearly independent? Why or why not?
A spanning set? Why or why not?
A basis? Why or why not?
Task 2: Craft this thing You will find crafting instructions on the last page. Label the faces, and on each face, label the vertices.
(b) Place the tetrahedron you crafted here and scan it with your homework. If you are writing on a tablet, include a photo.
Task 3: Find all the linear symmetries of the regular tetrahedron.
There are twelve of them, including the identity. Hint: The symmetries form a group. You can use the multiplication table below to help keep track of compositions.
(c) For each symmetry, give its matrix, and indicate its rotation axis and angle. You must enter exact values. It is recommended to write the common denominator in front of the matrix.
The identity linear transformation Id of R 3 has matrix
A → B → C
The symmetry sending A to B and B to C and C to A has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A ←→ B
C ←→ D
The symmetry interchanging A with B and C with D has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A → C → B
The symmetry sending A to C and C to B and B to A has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A ←→ C
B ←→ D
The symmetry interchanging A with C and B with D has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A ←→ D
B ←→ C
The symmetry interchanging A with D and B with C has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A → C → D
The symmetry sending A to C and C to D and D to A has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A → D → C
The symmetry sending A to D and D to C and C to A has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A → D → B
The symmetry sending A to D and D to B and B to A has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
A → B → D
The symmetry sending A to B and B to D and D to A has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
B → D → C
The symmetry sending B to D and D to C and C to B has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals
B → C → D
The symmetry sending B to C and C to D and D to B has matrix
Its rotation axis is the line spanned by the vector
Its angle of rotation about this vector, according to the right-hand rule equals