Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
FIN2020 HW6
Due: 2024/4/24 5 PM
Consider a one good, 2 periods (t=1,2) Arrow Debreu economy with 2 investors indexed by i=A, B. There are 2 states of the world indexed by s=1,2 and they have equal probability. The agents consume and receive endowment only at the second period. There is no endowment or consumption in the first period, though agents can trade in the first period. The endowments for agent A is eA = (1, 2) (i.e. 1 unit the of the consumption in state 1 and 2 units of the consumption good in state 2) and the endowment for agent B is eB = (2, 1). If agent A consumes the consumption plan CA = (c1(A) , c2(A)) and agent B consumes the plan CB = (c1(B) , c2(B)), the utility for agent A is given by
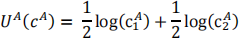
And the utility function for agent B:
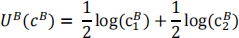
A.
Characterize the set of Pareto optimal allocations between the two agents. [Hint: You may need to consider the social planner with the weight 0< α <1 attributed to agent A preferences and the weight 1 - α to agent B preferences].
B.
We assume that it is possible to trade a set of Arrow Debreu securities that pay off one unit of consumption good if and only if a given state of nature occurs (two securities in total). We let p denote the price of an Arrow-Debreu security that pays off in state 1 and normalize to 1 the price of the Arrow-Debreu security that pays off in state 2. We are now set to determine equilibrium allocation and prices for this economy.
B (a).
Formulate the agent A investment problem given the securities prices and express the security demand as a function of the price p.
B (b).
Formulate the agent B investment problem given the securities prices and express the security demand as a function of the price p.
B (c).
Using the market clearing condition and questions B(a) and B(b), determine the equilibrium price of this economy and the resulting equilibrium allocation.
B (d).
Is the allocation Pareto optimal?