Faculty of Business and Economics
2021-2022 3rd Module Examination
MFIN6002ABCD
Spreadsheet Modelling in Finance
January 27, 2022 2:00pm —6:00pm
This is a take-home computer-based exam. There are 5 questions in total. Please read the instructions of each question in this exam paper carefully and finish all the questions in the Excel file.
When you answer the questions in Excel, you must include all the calculation steps in the worksheet.
Students can get access to internet, reference books and other teaching materials during the exam. Students must work on the exam independently.
Please submit the completed Excel file on the course Moodle before 6pm. Late submission will not be accepted.
Worksheet “ NFLX” contains monthly stocks data of Netflix Inc. (NASDAQ: NFLX) listed on NASDAQ from December 2012 to December 2020. Data are downloaded from Yahoo!Finance.
Worksheet “ FF4 Factors” contains monthly returns data of Fama-French 3 factors (market factor “Mkt- RF”, size factor “SMB”, book-to-market factor “HML”), momentum factor “Mom”, as well as monthly risk-free rates “RF” . Data are downloaded from Kenneth R. French’swebsite.
Momentum factor is defined as the difference between monthly average return on the high prior return portfolio and the monthly average return on the low prior return portfolio. The momentum factor refers to the tendency of winning stocks to continue performing well in the near term. Four-factor model including FF3 factors and momentum factor is widely used in the industry.
Use these data to answer Question 1 to 2.
Question 1 (15 points).
Go to Worksheet “Q1”. Use the raw data in Worksheet “ NFLX” and “ FF4 Factors” to answer the following questions.
(1) In columns C:G (highlighted range), calculate monthly data of four factors and risk-free which are ready for the multivariate regression (to estimate four-factor model).
(2) In column H (highlighted range), construct monthly log returns of NFLX stock from January 2013 to December 2020.
(3) In column I (highlighted range), construct monthly log excess returns of NFLX stock.
(4) Estimate the sample average, standard deviation, and correlation matrix of four pricing factors (Mkt- RF, SMB, HML, Mom). Report the results in highlighted ranges in columns L:O.
(5) Run the time series regression and estimate four-factor model for NFLX stock. The factor model is
Rt(e) = a + β1RM(e),t+ β2SMBt + β3HMLt + β4Mom t + et
where Re is excess return of NFLX stock, RM(e) is market excess return, SMB is size factor, HML is book-to-market factor, Mom is momentum factor.
In range L14:L24 (highlighted), use Excel functions to return the regression results, including a, β1, β2, β3, β4, residual standard error and t-statistics of hypothesis tests on each coefficient.
Note: You should NOT use Data Analysis Toolpak to generate regression results. You must enter one formula in each cell to immediate return the desired value.
Question 2 (25 points).
Go to Worksheet “Q2”. From Question 1 you may find that four pricing factors are correlated. Now we assume that NFLX stock excess returns satisfy the four-factor model
Rt(e) = a + β1RM(e),t+ β2SMBt + β3HMLt + β4Mom t + et
RM(e) , SMB, HML and Mom factors are correlated, and all the factors follow the normal distribution. Firm-specific shock ealso follows normal distribution and is independent of all the pricing factors.
In this question you will need to generate time-series simulation of NFLX stock returns and prices based on this four-factor model month-by-month over the next year.
(1) Goto VBA Module Q2. You first write a VBA function procedure named simuCorr(CorrMat as Range). The argument CorrMat is a Range object, defined as the correlation matrix of standard normally distributed random variables.
The output of the function procedure is a row vector of simulated random variables, all of which follow standard normal distribution, and the correlation matrix of simulated variables should be CorrMat.
Note: This is an array function. The size of the output range depends on the size of the argument. For example, if CorrMat is a 4 by 4 range, then output should be a row vector with four elements.
(2) Use VBA function procedure simuCorr to generate four correlated standard normal random variables (denoted as Z1, Z2, Z3, Z4) from month 1 to 12. The correlation matrix of Z1, Z2, Z3, Z4 is the estimated correlation matrix of four factors in Question 1(4). Report the results in range B5:E16.
(3) Calculate RM(e) , SMB, HML and Mom factors from the simulated Z1, Z2, Z3, Z4 in each. Report the results in range F5:I16.
Hint: You have estimated the average and SD of each price factor in Question 1. Use the estimated parameters in this calculation. In statistics, we learned that if a random variable X~N(μ, σ) then we can write X = μ + σZ, where Z~N(0, 1).
(4) Generate time-series simulation of firm-specific shockset, then calculate NFLX stock excess returns and stock prices from month 1 to 12. Report the results in range J5:L16.
Note: VBA function Cholesky is given in Module Cholesky_fn.
Feel free to include additional parameter estimations and intermediate calculation steps in this Worksheet if necessary.
Question 3 (25 points)
Go to Worksheet “Q3_4” . This question aims to use different option pricing models to calculate NFLX stock option price.
• We choose a call option written on this stock with strike price K = 520, and maturity date June 17, 2022. The option valuation date (today) is January 10, 2022. The market price of NFLX stock is $539.85. Information is listed in Excel as well.
• NFLX never paid dividends.
• Daily market data of NFLX stock in the past 1 year are downloaded from Yahoo!Finance and saved in Worksheet “ NFLX(option)” .
• 4-week Treasury Bill rates, 3-month Treasury Bill rates, and 6-month Treasury Bill rates in the past month are downloaded from St. Louis Federal Reserve website and saved in Worksheet “ RiskFree(option)” .
(1) Complete the input table in range B12:B19 (highlighted). You can decide the time unit in the estimation of input parameters, and how to measure returns from the daily NFLX price data.
(2) In VBA Module Q3, VBA functions CND, BS, and Binomial_all are given. An important proposition in option valuation states that the price of an American call option is equal to the price of the corresponding European call if the underlying stock does not pay the dividend.
In this question, NFLX stock does not pay the dividends. Therefore, the European option price and American option price should be equal.
In cell B23, use BS function to calculate the price of this option based on Black-Scholes model.
In cell B25, use Binomial_all function to calculate the option price based on CRR binomial tree.
(3) In CRR binomial tree with n periods, denote time to maturity as T. Then the total returns of up move and down move are given by
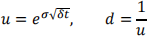
where δt = n/T. The risk-neutral probability of up move is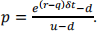 
.
At maturity date (at step n), in state i (defined as the total number of down moves from step 0 ton), the stock price is given by
Sn(i) = S0u(n−i)di, for i = 0, … , n
The probability that state i occurs is
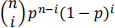
where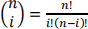 
is binomial coefficient. Excel function Combin(n,i) gives values for the binomialcoefficients.
Based on risk-neutral valuation method, the current price of a European option is the discounted value of expected payoff at maturity:
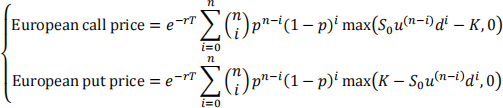
In VBA Module Q3, complete VBA function procedure Binomial_euro_new and use above equations to calculate European call and option prices.
Use this VBA function in cell B26 to calculate the price of this option. (The result should be the same as using Binomial_all function).
Question 4 (25 points).
Monte Carlo simulation can be applied in the option valuation. In this question we use simulation method to price a European option. We assume that the price process of the underlying stock is geometric Brownian motion under the risk-neutral measure:
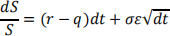
Then the stock price after time T is given by
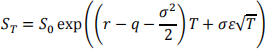
where S0 is the current stock price, T is time to maturity, r is the continuously compounded risk-free rate, q is the continuous dividend yield, and σ is the volatility of the underlying stock.
The option payoff depends on the stock price at maturity, ST. For the call option, the payoff is max (ST − K, 0); for the put option, the payoff is max (K − ST, 0), where K is the strike price.
The current option price is calculated as the expected payoff at maturity T, discounted by risk-free rate over the same period, that is e−rT .
(1) In VBA Module Q4, write a sub procedure called MCMOption that takes the following actions:
• Read the input parameters in ST equation from the input table in Worksheet “Q3_4” to the sub procedure.
• Generate 200 simulations of stock prices at maturity date (time T) and write the simulated stock prices into Range B35:B234 in Worksheet “Q3_4” .
• Calculate option terminal payoffs based on the 200 simulated stock prices and write the payoffs in Range C35:C234.
(2) Go back to Worksheet “Q3_4” . In cell B31, calculate this option value based on the simulated option terminal payoffs in Range C35:C234.
Question 5 (10 points).
Go to Worksheet “Q5”. In the lecture,we have shown how to construct delta hedging portfolio of a European option and calculate the payoffs of hedged portfolio.
We decide to replicate an at-the-money European call option that has 12 weeks to run until expiration.
The stock on which the option is written has S0 = $50 and strike price k = $50, the interest rate is r = 4% per annum, continuous dividend yield is q = 0 per annum, and stock volatility is σ = 40% per annum.
We construct delta hedging portfolio of this option week-by-week till maturity date, based on the Black- Scholes-Merton model:
Call price = Se−qT N(d1) − ke−rT N(d2) = SΔcall− ke−rT N(d2)
where
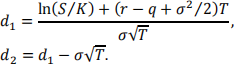
In the Black-Scholes model, the price process of the underlying stock is geometric Brownian motion under the risk-neutral measure:
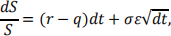
and the stock price after δt (1 week in this example) is given by
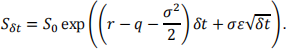
(1) The input parameters of the option and calculation of delta hedged portfolio payoffs in each week have been provided in the Worksheet (same as in the lecture).
VBA functions SimGBM and BSDelta are given in Module Q5.
At maturity date,what is the hedged portfolio payoff? Report the result in cell B31 (highlighted).
At maturity date, what is the actual payoff of this call option? Report the result in cell B33 (highlighted).
(2) Use Data Table function to repeatedly generate the payoff of the hedged portfolio and the call option at maturity for 10 times. Report the cross-sectional simulation results in highlighted range C37:D46. Calculate the averaged difference between two payoffs based on 10 simulations in cell D48.