Hello, if you have any need, please feel free to consult us, this is my wechat: wx91due
MAT 150A HW01
Reminder. Your homework submission must be typed up in full sentences, with proper mathematical formatting. The following resources may be useful as you learn to use TeX and Overleaf:
• Overleaf ’s introduction to LaTeX: https: // www. overleaf. com/ learn/ latex/ Learn_ LaTeX_ in_ 30_ minutes
• Detexify: https: // detexify. kirelabs. org/ classify. html
Covered in this HW Parts of Chp. 1, esp. §1.5, 2.1–2.4. Matrices, rotations, definition of a group, symmetric groups and permutations, etc.
Grading Some of the (parts of) problems will be graded in detail out of several points, and necessary feedback will be given. The rest will be graded out of 2 points. I will reveal which problems are fully graded in the solutions, which will be posted on the Friday following the due date.
Exercise 1
In Lecture 1, we described a group G generated by rotations of θ = π 4 about the x-, y-, and z- axes. To be more precise, we set a convention for the coordinate axes
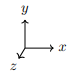
(e3 points out of the board)
and wrote down the associated matrices for our chosen generators:

Since θ = π 4 , cos θ = sin θ = √ 1 2 := t, so we can rewrite our matrices as follows:
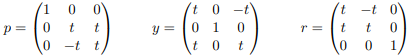
We used spatial reasoning to try to find a sequence (composition) of the actions (elements of G) p, p−1 , y, y−1 that is equal to r; this would prove that only G is generated by {p, y}, and in particular, r is not needed as a generator. Some guesses included p 2y −1p −2 and py−1p −1 .
Typesetting tip: To typeset matrices, copy and paste my code for typesetting matrices above, then modify the entries.
(a) Find matrices representing p −1 and y −1 ; prove that these are indeed inverses to p and y, respectively.
(b) Use matrix multiplication and trigonometric identities to compute p 2y −1p −2 and py−1p −1 . Which of these, if any, is equal to r?
Exercise 2
In this exercise, you will explore the symmetric group on 4 indices, S4. First, read page 42 of the text to see how S3 is described. Lecture 2 and the accompanying note may also be useful.
Warning The text defines a transposition to be any 2-cycle (i j). In class, we restricted this definition to 2-cycles involving only adjacent indices, i.e. τi = (i i + 1).
(a) Write the permutations p = (1 2 3 4) q = (1 3 2 4) r = (1 4 2) as products of (adjacent) transpositions τi .
(b) In class, we discussed why the set of transpositions {τ1, τ2, τ3} generate S4 intuitively, but we did not prove it:
Proposition (A). The symmetric group Sn is generated by the set of (adjacent) transpositions {τ1, τ2, . . . , τn−1}.
Assuming Proposition A is true, prove that S4 is generated by {(1 2),(1 2 3 4)}.
Hint: Can you show that τ2 and τ3 are generated by these two elements?
Exercise 3
This exercise focuses on permutation matrices and determinants. For a refresher on determinants, see §1.4 in the text. In particular, we will need the following facts, labeled here as Lemmas A and B:
Lemma (A). The determinant of the n × n identity matrix In ∈ Mn×n(R) is 1.
Lemma (B). If M′ is obtained from M by interchanging two different rows, then det A′ = − det A.
We will also need the following definition:
Definition (Sign of a permutation). Let p ∈ Sn be a permutation. The sign of p is equal to the determinant of the permutation matrix P representing p: sgn(p) := det(P).
(a) Prove that the transpose of a permutation matrix is its inverse.
(b) Prove that the determinant of a permutation matrix is always ±1. Therefore the sign of a permutation is always either +1 or −1. If sgn(p) = +1, we say that p is even; otherwise, if sgn(p) = −1, we say that p is odd.
(c) Let p ∈ Sn, and write p as a composition (or equivalently, product) of k transpositions:
p = τi1 ◦ τi2 ◦ . . . ◦ τik
Prove that p is even if and only if k is even, and that p is odd if and only if k is odd. In other words, we could define sgn(p) to be (−1)k , where k is the number of transpositions in any composition of transpositions equal to p.