January 2022 Examination Period
Department of Computer Science
3rd Year Examination for the Degrees of
Bachelor in Computer Science
Master of Engineering in Computer Science
COMS30033
Machine Learning
Part 1: Short questions (5 marks each)
Question 1 (5 marks)
What are the key differences between the different forms of machine learning (unsuper- vised, supervised and reinforcement learning)?
Question 2 (5 marks)
Which of the following models (Figure 1) overfit or/and underfit the data and whg?
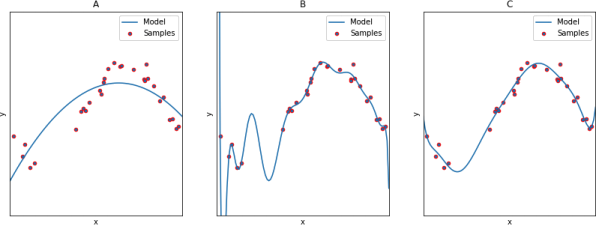
Figure 1: Examples of data (red scatter plot) with three different models (A,B,C; blue solid line).
Question 3 (5 marks)
Figure 2 shows a Bayesian network structure (i.e. directed acyclic graph). Write down all pairs of variables which are independent conditional on A.
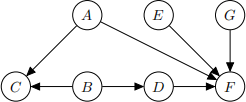
Figure 2: Directed acyclic graph for Question 3
Question 4 (5 marks)
Let S be the sample covariance matrix of some data where S is:
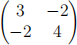
Let u1 = (−0.6154, 0.7882) be the first principal component of the data (approximated to 4 significant figures). What is the variance of the data when projected onto one dimension using this principal component? (Give you answer using 4 significant figures.)
Question 5 (5 marks)
Consider running the Metropolis-Hastings algorithm where the target distribution p is a mixture of Gaussians and we use a symmetric proposal distribution. Let zt be the current state and let z* be a proposed new state. Suppose that p(z* ) ≥ ϵp(zt ) for some value ϵ > 0. If possible, write down the acceptance probability as a function of ϵ, otherwise explain why it is not possible.
Question 6 (5 marks)
Suppose you were using EM to estimate the parameters of a mixture of 3 Gaussians. Let xi be a training datapoint where Ⅵ (xi |µ1 , Σ 1 ) = 0.3, Ⅵ (xi |µ2 , Σ2 ) = 0.4, Ⅵ (xi |µ3 , Σ3 ) = 0.2. µj and Σj are the current parameter values for the jth Gaussian. Suppose the current parameter values for the mixing coefficients were π1 = 0.2, π2 = 0.4 and π3 = 0.4. Compute (up to 3 significant figures) the responsbility γij for j = 1, 2, 3, i.e. the probability that xi was generated from the jth Gaussian.
Question 7 (5 marks)
Here is a dataset with 2 datapoints where each row is a datapoint:

Let ϕ1 (x) = xTx and ϕ2 (x) = x1 − 2x2. Write down the Gram matrix for this data using the kernel associated with the feature map ϕ where ϕ(x) = (ϕ1 (x), ϕ2 (x)).
Question 8 (5 marks)
You are using a linear dynamical system to predict a continuous state variable, zn. For
p(zn |x1 , , xn−1) = Ⅵ (0, 202), (1)
with mean of zero and variance of 202. You observe a noisy measurement of the state, xn = 50, where xn = zn + ϵn and the noise ϵn is zero-mean, Gaussian distributed:
p(ϵn ) = Ⅵ (0, 12 ). (2)
You use the Kalman filter to update your distribution over zn , giving you a posterior:
p(zn |x1 , ..., xn ) = Ⅵ (µ, σ2 ). (3)
(a) Is the value of the posterior mean, µ, closer to 0 or 50?
(b) Is the value of σ greater or less than 20?
Question 9 (5 marks)
Bagging trains classifiers on different subsets of the dataset. How can this improve the performance of the ensemble?
Question 10 (5 marks)
Crowdsourcing is often used to annotate datasets for training and evaluating machine learning systems. List at least three ways in which we can improve the quality of the labels obtained from crowdsourcing.
Part 2: Long questions (10 marks each)
Question 11 (10 marks)
You are given a very simple neural network (Figure 3) with only one input x and one output neuron y with a sigmoid activation function σ . Consider that the network is currently receiving the following data point x = 0.1 and that its target should be t = 1. Assume a standard mean squared error, E = 2/1(y - t)2.
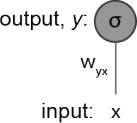
Figure 3: Schematic of a simple artificial neural network.
(a) To perform gradient descent on the weights in your network you must compute wgx = wgx − δ![]() yx(E) . What is the numeric value for δ
yx(E) . What is the numeric value for δ![]() yx(E)? Assume that the current wgx = 0.9 and that there is no bias. Your answer only needs to be approximate (e.g. 0.06 instead of 0.062348). Make sure to explain the equations and steps used to arrive at your solution. (5 marks)
yx(E)? Assume that the current wgx = 0.9 and that there is no bias. Your answer only needs to be approximate (e.g. 0.06 instead of 0.062348). Make sure to explain the equations and steps used to arrive at your solution. (5 marks)
(b) What is the curse of dimensionality and how do artificial neural networks models deal with it? (3 marks)
(c) Are artificial neural networks parametric or non-parametric models?
Explain whg. (2 marks)
Question 12 (10 marks)
One option when learning the parameters of a Gaussian mixture model is to use EM to (attempt to) find the maximum likelihood estimates of the parameters. In this question we consider an alternative Bayesian approach
(a) Draw the Gaussian mixture model as a Bayesian network using plate notation. Do not forget to include nodes which represent the model parameters. It is fine to use a single node to represent a random variable which has matrix or vector values. State which nodes of your Bayesian network are observed and which not. You do not need to represent the number of Gaussians in the mixture model. You do not need to define priors over model parameters. (5 marks)
(b) One way to get an approximation to the posterior distribution over model parame- ters is sampling: either sampling from the posterior distribution itself or sampling from a sequence of distributions that get ever closer to the posterior distribution. Consider (i) rejection sampling and (ii) MCMC as methods for approximating the posterior distribution for a Gaussian mixture model. Give pros and cons of each method and state which method is preferable for this problem. (5 marks)

Figure 4: SVM results for Question 13
Question 13 (10 marks)
(a) Fig 4 shows the results (in the implicit feature space) of learning with an SVM. The separating hyperplane is in red and the margin is indicated by the blue lines. Training datapoints x1 , x2 , x3 and x5 have class label −1 and training datapoints x4 , x6 , x7 and x8 have class label 1. x7 is correctly classified. Which data points are misclassified and which are support vectors? (5 marks)
(b) The following minimisation problem (or an equivalent formulation) is solved when using SVMs with soft margins:
 (4)
(4)
Explain what each of the symbols represents and how altering the value of C affects an SVM classifier. (5 marks)
Question 14 (10 marks)
This question is about hidden Markov models (HMM). We have a discrete text sequence labelling task with three classes. You have trained a hidden Markov model (HMM) using expectation maximization (EM) and obtained the following estimates of the initial state probabilities, π, and transition matrix, A:
 (5)
(5)
Rows in A correspond to values of zn and columns to values of zn+1 .
The likelihood of each token in the vocabulary, xn, given the state, zn, is given by an emission distribution matrix, which you have also learned already using EM. In this matrix, the rows correspond to the token values, i and the columns to the state values, j. The emission distribution matrix is shown here:

Suppose you observe the following short sequence of text tokens: ["In", "Senegal"]
(a) Compute the probability p(z1 |x1 = “In ” , x2 = “Senegal”) to three decimal places.
(b) True or false: the Viterbi algorithm is an alternative to the forward-backward al- gorithm. Explain your answer in one or two sentences.
Question 15 (10 marks)
This question is about CART decision trees. Suppose we want to train a classifier to decide whether an email is important to a user or not given three features. data is shown below, where each row contains the data for one email:
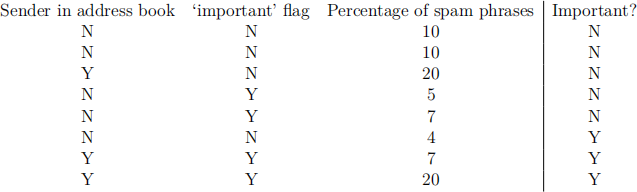
(a) Suppose we learn a CART decision tree, where the objective used to grow the tree is to minimise cross-entropy error. No pruning is used. Draw the final learned tree and state the amount of residual error.
(b) What is pruning and why is it often used with decision trees?