COMP2221 Programming Paradigms

* This is the deadline for all submissions except where an approved extension is in place.

Late submissions received within 5 working days of the deadline will be capped at 40%. Late submissions received later than 5 days after the deadline will receive a mark of 0.

It is your responsibility to check that your submission has uploaded successfully and obtain a submission receipt.

Your work must be done by yourself (or your group, if there is an assigned groupwork component) and

comply with the university rules about plagiarism and collusion. Students suspected of plagiarism, either   of published or unpublished sources, including the work of other students, or of collusion will be dealt with according to University guidelines (https://www.dur.ac.uk/learningandteaching.handbook/6/2/4/).

2. Problem Definition

The Shortest Vector Problem is the most famous and widely studied computational problem on lattices. A Lattice is a discrete and  periodic grid-like structure formed by linear combinations of a set of basis vectors in n-dimensional Euclidean space. The key characteristic of a lattice is that it extends infinitely in all directions. In the context of computational  mathematics and computer  science, lattice problems often refer to tasks related to these lattice structures. Common lattice problems include finding short vectors within a lattice, which is the Shortest Vector Problem (SVP).

The SVP problem that you need to solve through your implementation as part of this assignment is as defined as follows:
Given a lattice structure L embedded in n-dimensional Euclidean space ℝn,where L is generated by a set of linearly independent basis vectors {b1,  b2,  ...,  bn}, the objective is to identify a nonzero lattice vector v ∈ L such that the Euclidean norm (L2) of v is minimised. In short:

Find v ∈ L,  v ≠ 0, such that ||v ||₂ is minimised,

where  ||v ||₂  is  the  Euclidean  norm  of vector v, defined as: 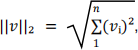 where vᵢ represents the components of vector v in the n-dimensional space.

Your goal is to implement a solution to this problem at an arbitrary number of dimensions n with considerations for runtime and memory requirements.

3. Hints

Here are a few hints to help get you started:

●    Please  read  the  submission   instructions  carefully.  Since  this   is  a  programming assignment, deviations from the  instructions  might  lead to you  losing  marks as a result of simple submission mistakes that can lead to your submission not running.

●   Your implementation should  be as efficient in its performance as possible, both in terms of memory and run-time.

●    It is important that your solution can generalise to an arbitrary number of dimensions. You can start with a fixed small number of dimensions, like two, and then try to adjust your implementation to perform within an n-dimensional space.

●   Creating the right data structures to hold your vector components and functions that perform  the  required  operations  on  your  vectors  can  make  your  implementation easier.

●   You  can  implement a brute-force search to  solve  this  problem.  Enumerate  all possible combinations of lattice vectors to find the shortest one. Keep track of the shortest vector found so far.  Keep  in  mind that this  brute-force approach can  be highly inefficient and impractical for high-dimensional lattices, and of course, your implementation  might  be  tested  on  a  higher  number  of  dimensions.  As  a  result, optimising the process is very important since part of the marks is given based on performance and memory requirements.

●   With the right optimisation, you can potentially get the full marks by implementing a brute-search approach. However, you can opt for more advanced algorithms.

● You are not expected to develop novel algorithms, but there is a class of lattice reduction methods that can  provide solutions  in a  much faster and more efficient manner than a brute-force search. Additional credit may be given for the use of more advanced  algorithms.  Consider  the  trade-off  between  memory  and  speed, when implementing advanced methods. A simple enumeration technique for an exhaustive search might use much less memory than a faster and more complex algorithm and can be easier to optimise.

●    Implement error handling and bounds checking to ensure that your program handles invalid input, doesn't go into an infinite loop or other such issues. Not only will this make your implementation easier to test for yourself but is also part of the marking scheme and can affect your marks.

●   Optimise   your   code    for   performance,    especially    if   you    are   dealing    with high-dimensional  lattices.  This  might  include algorithmic optimisations and careful memory  allocation.  Make  sure  your  optimisation  methods  are  explained  in  your report.  Advanced   optimisation  methods  will  receive  extra  credit.   Be  mindful  of memory usage, which is especially important in high-dimensional problems. Allocate and deallocate memory efficiently to avoid memory leaks.

●   Test your implementation with known lattice problems where you already know the solution to verify its correctness. see https://www.latticechallenge.org/svp-challenge/ You can also try your solution on a "Lattice D", often denoted as Dn . It is one of the simplest  and  most  fundamental  lattices  used  for  benchmarking  and  testing  SVP algorithms.  It  serves  as  an  excellent  starting  point  for  understanding  the  basic concepts of lattice problems and their solutions. Lattice Dn  is an n-dimensional lattice formed by the integer combinations of the standard basis vectors in n-dimensional Euclidean space.  In other words,  it consists of all vectors whose components are integers.  The  basis  vectors  for  Lattice  Dn    are  the  standard  unit  vectors.  In  two dimensions (D2), you have basis vectors [1, 0] and [0, 1], while in D3 , you have basis vectors [1, 0, 0], [0, 1, 0], and [0, 0, 1], and so on. The shortest vector is always the shortest basis vector, which has a length of 1. This can be used as a benchmark to evaluate the correctness and efficiency of SVP-solving algorithms. Since the solution is known, you can verify if your algorithm correctly identifies the shortest vector.

●    Understand the time and space complexity of your implementation to estimate its performance for different problem sizes. Cover this in your report.

●    Make sure you submit your files well before the deadline to make sure that system or network issues do not affect your submission. Every year, we receive dozens of

emails right after the submission deadline from students with their submissions

marked as “late” due to a variety of reasons. Do not leave your submission to the

final minutes and leave yourself plenty of time to deal with any issues that might

affect your submission. Note that lecturers do not have the power to grant extensions and late submissions are handled by the office centrally.

4.  Code and Submission Specifications

●   Your program Your code should run on Linux. A Docker imageof Ubuntu 22.04 with `apt-get install -y gcc` will give you an identical environment to the one used for marking. Alternatively, you can  use the University Linux system Mira. Failure to do so may result in all marks being lost   regardless of whether it compiles and runs on your own windows machine. Note the Mira might occasionally experience downtime due to maintenance or other potential issues.

The deadline will not be extended due to issues with Mira or other university provided systems. You are able to complete the implementation using the Docker image as explained above.

● You are allowed to use either C or C++ for your implementation.

● You are not allowed to use any external libraries but you can use all standard headers.

Only use the headers that are needed. Do include what is not necessary as that will affect your marks.

●   You may have as many source files and headers files as you need - considering that your code should be organised well and easy to follow - but your program should be run via an executable called `runme`, which should be produced by your program. This executable   should only be called `runme` and should not have any extensions.

● You will need to include a Makefile and your Makefile should include an `all` option, which compiles all the necessary source files and headers that you submit and creates an executable  ` runme`. Our automated marking script will try to compile your program to get the executable by running the command `make all`.

● Your Makefile will be marked for functionality, clarity and correctness. Your Makefile should also contain `test` and `clean` options that respectively test the program with a known lattice and clean the compile environment.

●   Your executable should be able to receive an arbitrary number of input arguments. These input arguments will correspond to the basis vectors that define the lattice. For instance,   your program will be tested by running the following command:

` ./runme [1 .0 0 .0 0 .0] [0 .0 1 .0 0 .0] [0 .0 0 .0 1 .0]`

In this example,  I  have  passed three three-dimensional basis vectors as inputs to your program. Other more complex vectors will be used to test your submission.

●   The arguments will be passed and should be read in the format of the example you see above. There will always be the same number of input vectors as their dimensions. Your program should parse the arguments, infer the number of dimensions, and solve the shortest vector problem.

● Your program should be able to handle incorrect argument formats and numbers.

●   The basis vectors passed in as input arguments to define the lattice can have real numbers as their components.

●   The output of your program should be the length (2  norm) of the shortest vector as a     scalar. You should not output the vector components but just the length. Your program    must save the output of your program in a text file called  `result .txt`. Your program should create this text file and just save one number, the final answer that your program generates, in that file.

●   Some of these code specifications will be checked automatically on Gradescope after you submit your files. If Gradescope is showing that you have submitted your files in the wrong format and they cannot be  run, this means that your assignment will not be marked, and you will receive a mark of zero. Make sure you submit your files well before the deadline to make sure that they are in the right format, and you have time to re-adjust so they can be run  correctly.Do not ignore the errors and  warnings  from Gradescope.

●    If your program does not compile and generate the correct executable named  ./runme and is not run via the command (with this of different arguments passed in this format)

` ./runme [1 .0 0 .0 0 .0] [0 .0 1 .0 0 .0] [0 .0 0 .0 1 .0]`

or does not generate the   ` result .txt` file with the final solution inside, you will lose marks or might get a mark of zero.

● You are responsible for how your submission files are uploaded to Gradescope – e.g., by zipping and submitting everything or submitting files individually. No guidance is provided on this matter. Make sure you submit your files well before the deadline to make sure that they are handled by the Gradescope system correctly.

●    Do  not submit any extra files. Compressed files, git related files, files produced by the Mac operating system if that is what you are using (e.g., DS_Store or other files) or any other unnecessary files will result in your submission being marked down.

5. Submission

●    Full program source code files for your final solution to the above task as a working C or C++ program, meeting the above “code and submission specifications” for testing.

● You must submit the following files:

。 All source and header files that are needed to compile your program.

。 A Makefile that has the `all`, `test` and `clean` options and will compile your program and generate the ` runme` executable.

。  Report (max. 750 words) detailing your approach to the problem and the success of your  solution  in  the  task  specified.  Provide  any  illustrative  figures,  diagrams  and tables (as many as you feel necessary) of the performance of your solution. Any diagrams, images, titles, captions, tables, references, and graphs do not count towards the total word count of the report. Summarise the success of your system in   performing  the  required  task,  speed  during  run-time  and  reducing  memory requirements. Your report can follow any structure as long as it is clear and easy to follow. Submit a  PDF  (not  in any other format). Your submission will be marked down if any file format other than a pdf is submitted as the report.

6. Marks

The marks will be awarded as follows:

● Correctness of the solution          15%

○   You may receive partial marks for certain parts of the solution  but note that certain wrong solutions might lead to the loss of   not only the entirety of this portion of the marks but other parts as well.

●    Makefile                               5%

○   Your Makefile should have `all`, `test` and `clean` options and will be marked based on correctness, functionality and generalisability.

●    Performance of your program in terms of run-time (speed)                  10%

●    Performance of your program in terms of memory requirements          10%

● Quality of the implementation

○   Clear, readable, well-documented (with sufficient comments) and well-presented program source code      10%

○    Error handling    5%

○    Extensibility        5%

●    Report:

○    Discussion/detail of solution design and choices made           10%

○ Quantitative evidence and analysis of performance           10%

● Additional credit for one or more of, but not limited to, the following:

○ design and use of an alternative or novel methods